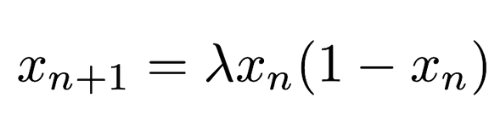Summary
This week my writing got a little longer than usual and moreover I didn’t have a particularly interesting book to review so I’ve kept this post to only the essay. Next week will return to the usual essay & book review combo.
Your simple model of the world may contain unexpected results
For the last couple of weeks I have been exploring the logistic map in a Jupyter Notebook1. The logistic map is an equation often used to model the population of a species as it changes over time. The population in the next period (𝒙_n+1) is a function of the population in the current period (𝒙_n), and a growth rate term lambda (𝜆). The population is always a value between 0 and 1, as a percentage of the environment’s carrying capacity.
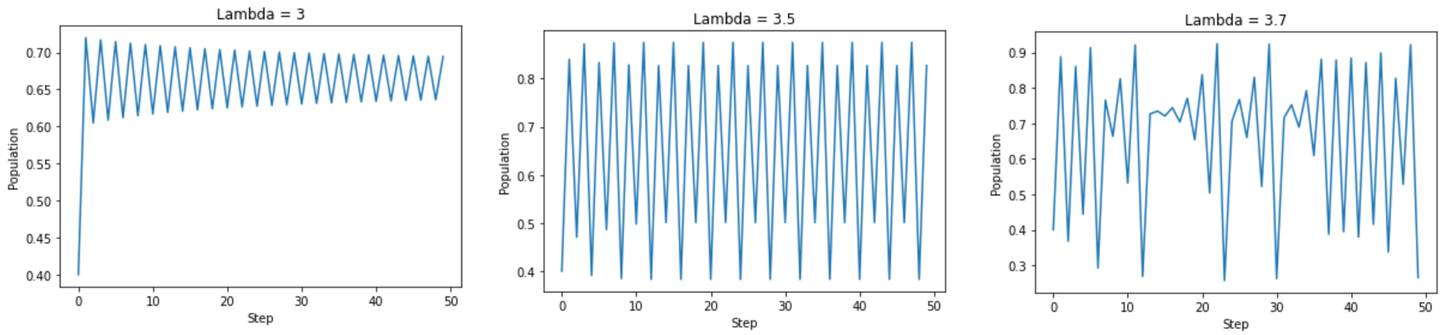
In the scheme of things, the logistic map is an uncomplicated equation. Just one variable and one parameter. However, it has some surprising properties. At first, when lambda is around 2 the long-term population settles into a steady state. Intuitively, you can think of this as the population reaching equilibrium with its surroundings. As lambda becomes greater than 3 however, the population begins to oscillate between a couple of states developing a kind of boom and bust behaviour. Eventually, around a lambda of 3.7 the population transitions to chaotic behaviour. From this point on, the population refuses to settle into an identifiable pattern2.
We simplify the world using models to make sense of what is going on around us. This can be really quite useful. Clear frameworks demystify complicated situations and allow us to predict the future. However, the logistic map shows that even if our model is entirely correct, as the parameters change, we can end up in fundamentally new paradigms with unpredictable behaviour that we may not be ready for. We have trained our intuition on the behaviour in an existing regime (e.g. a particular value of lambda) and as things shift these intuitions can be strained.
Let's say we have a Saas company, General Software Services Inc. Our business model is exceedingly simple: we create a software product and sell other companies subscriptions to use it. Due to the zero marginal cost of replication for our software and the large fees we charge this is a very profitable endeavour. We’re a relatively new company and if we add product features that customers ask us for and hire sales people to sell to more of the world's largest 500 companies we will continue to grow and become increasingly profitable. This model is pretty accurate and a good way to predict what will happen with the business. However, let's say we have actually sold to 80% of the Fortune 500 and we have crushed the product roadmap with more than 100 features added to our platform - what happens then?
As we approach this limit, our model remains accurate but the behaviour of the company can start to turn in very strange directions. We thought that our past behaviour: add more features, hire more salespeople was all we ever needed but it turns out there are many other requirements to our long-term success. For one, we should hire a lot more lawyers.
We have good models of the world. We use these models every day and become used to the way they usually operate. But we mistake the way that the model behaves now for the model itself. To prepare for the future it is worth imagining where our model could take us were the environment to change.
Thanks to Casey Li for reading a draft of this newsletter.

I highly recommend reading the linked article in full as there is much to be learned from the equation. In case it is useful for anyone who wants to similarly explore the behaviour I have also put up my notebook here. It comes with two warnings. 1) I have not spent a significant amount of time programming. If you are someone who has, then some of the code I've written may make you cringe. 2) If you are unfamiliar with Jupyter notebooks or similar environments they can be quite overwhelming. If you are looking for a more straightforward way to understand what the equation is and how it operates I recommend reviewing the article.
This is not precisely right. Perhaps even more shocking than the chaotic behaviour that develops is that for certain values of lambda in the chaotic zone the logistic map briefly returns to steady oscillating patterns, you can explore this in the linked article.